NIRS of chocolate and its chemometric analysis

In today’s modern society, chocolate has been established as a premium lifestyle food product. Besides oil and coffee, cocoa is one of the most valuable commodities of global trade. About four per cent of cocoa beans traded on the world market originate from the noble criollo bean and are the basis of the so-called premium grand cru products (for more information, see www.icco.org). Due to fluctuating prices on the stock market and a current high price close to USD 2500 per tonne, chocolate manufacturers demand an efficient, reliable and speedy method for product and quality control. We report here on the analysis of cocoa with the help of near infrared (NIR) spectroscopy in the wavenumber range from about 4000 to 12000 cm-1 combined with chemometrics to determine the fat, protein, sugar and water content in chocolate base.

It is not just the flavour components of chocolate that largely influence the quality of chocolate – fat, protein, sugar and water also contribute to the desired mouth-feel, melting behaviour and flavour release. The quality of chocolate is significantly influenced by the content of the four constituents, namely fat, protein, sugar and water. It is, therefore, of great importance to develop and refine precise and reliable analytical methods to determine their amount in chocolate. The concentrations of these components are currently largely determined through costly analysis by external laboratories, which also delays the production process. This was the motivation to search for other methods which are reliable and fast because they can be performed in-house. The recommended methods to determine the content of fat, protein, sugar and water have been described1. Each of the four constituents is determined by time-consuming recommended analytical procedure. The triglycerides content is determined by soxhlet extraction and requires several hours. Protein content is analysed using the Kjeldahl method, while water content is determined by Karl-Fischer titration or by oven drying over several hours. The concentration of sucrose is investigated by means of an enzymatic reaction. These recommended and rather complicated methods are performed by specialised analytical laboratories, guaranteeing a standard evaluation. They are rarely useful to monitor the production process since samples would have to be collected during the production and sent to the laboratory for a detailed analysis. In addition, most chocolate manufacturers do not have the necessary personnel and infrastructure to carry out internal analysis. Therefore, companies are forced to outsource. A very early special motivation was the idea to replace difficult and demanding sensory analysis by simple and reliable measurements2.

A spectroscopic alternative

Due to the limitations of the classical wet chemical analysis just described, it is desirable to develop quick, less expensive, reliable methods. Obvious alternatives to the classical methods are those involving spectroscopy. Near-infrared (NIR) spectroscopy is used widely in the food industry and increasingly for cocoa analysis3-6. NIR spectroscopy uses the electromagnetic radiation in the near-infrared spectral range to induce vibrational absorptions in molecules. The energy of the NIR light ranges from 4000 cm-1 to approximately 12500 cm-1 for the quantity wavenumber (symbol v~) corresponding to the quantity wavelength (symbol λ) between 2500 nanometres and 800 nanometres.

When a sample is irradiated with electro – magnetic radiation, the molecules can absorb photons and subsequently undergo a transition from a vibrational state of lower energy to a vibrational state of higher energy. In the NIR range, mainly transitions in overtones and combination bands are observed.

Hence, if a sample is irradiated with infrared light of intensity I0, a part of the light will be absorbed and the emergent radiation I will be weaker. The absorbance A as the logarithm of the ratio of incident over transmitted intensity, A = In(I0/I), of a substance is described by the Lambert-Beer Law (Equation 1) and is linearly related to the concentration c of the substance in the sample:

Eq 1

A is the absorbance, ε is the molar extinction coefficient (unit: L mol-1 cm-1), l is the path length (unit: centimetre), and c is the concentration of the substance (unit: mol L-1)7. This linear relationship between absorbance and concen – tration is ideal for quantitative analysis, this holds with slight modifications also for transmission or reflectance measurements7. Since NIR spectra are usually characterised by broad, more or less unstructured and over – lapping bands, their quantitative analysis requires some knowledge of NIR spectroscopic interpretation and relies strongly on chemometrical evaluation methods.

Chemometrics

According to IUPAC (International Union of Pure and Applied Chemistry, www.iupac.org) Chemometrics is ‘the application of statistics to the analysis of chemical data (from organic, analytical or medicinal chemistry) and design of chemical experiments and simulations’8. The term chemometrics was coined by Svante Wold in 1974 and since then has developed “to an integral part of all areas of chemistry”9. Chemometrics is applied with great success in pattern recognition and classification, structureactivity modelling, design of experiment, multivariate process modelling and monitor – ing10-13. An important chemical application of chemometrics is to determine the amount of constituents within a sample, for example, the content of fat, protein, sugar and water in chocolate3-6. In the NIR spectrum, each con – stituent has a certain wavenumber range which shows characteristic absorption features that can in turn be used to determine its concen – tration in the sample after suitable calibration procedures. Unfortunately, the NIR spectrum often shows overlapping bands which renders the analysis more difficult. It is therefore advisable to make use of chemometric methods where multivariate calibration (using many probes at many wavelengths or wavenumbers) is possible. Multivariate calibration has become necessary and helpful in analytical chemistry for the evaluation of spectrometric data as it offers tremendous advantages over the classical one-wavelength approach (many probes at one wavelength or wavenumber). Although comm – ercial software packages exist to perform chemometrical analysis, a basic knowledge of mathematics, matrix methods and statistics is mandatory to understand chemometrical methods and avoid fallacies. In the case of chocolate, a huge amount of data is collected: fat, protein, water sugar and various concen – trations of the constituents depending on the probes including NIR spectra collected over a broad wavenumber range with specified spectral resolution. Multivariate methods are well suited to bring order into the enormous amount of data collected and to help interpret the data graphically. When concentrations need to be determined, calibration data is collected and regression methods are used to determine concentrations of probes with unknown content. The concentrations are determined indirectly by measuring the NIR absorption, which is expected to follow Lambert-Beer’s law.

Among the most popular multivariate method is the so-called Principal Component Analysis (PCA) for data reduction and classifica – tion. When regression comes into play, the Principal Component Regression (PCR) and the Partial Least Squares Regression (PLS) are applied within the multivariate method. While PCR can be considered as an expansion of PCA as it regresses Y-data (e.g. concentrations) on X-data (e.g. absorbance) that have previously been transformed with PCA, PLS can be seen as a further development of PCR, in that not only the X-data but also the Y-data undergo a sort of PCA-transformation.

Brief introduction to PCR

In the framework of PCA, an NIR spectrum can be considered as a single point in a multidimensional coordinate system, where a coordinate corresponds to a specific absorbance at a particular wavenumber. For example, if one measures seven different samples of chocolate at two different wavenumbers, v~ and v~ 2, the 14 different NIR absorptions are represented as seven points in a two-dimensional coordinate system spanned by the two absorbances, A1 and A2, respectively (see Figure 1 for an artificial set).

Figure 1: PCA model for seven different samples measured at two different wavenumbers (v~ 1, v~ 2). The seven different NIR spectra are shown as seven points in the (A1, A2)-plane. PC1 and PC2 represent new orthogonal, rotated axes along the directions with the largest (PC1) and the second largest (PC2) variances

The PCA now rotates the co – ordinate system so that the maximum possible variance of the points lies along the first axes (principal component 1, PC1), whereas the second principal component (PC2) describes the variance not already described by PC1; PC2 is orthogonal to PC1. From a mathematical point of view, PCA is the solution of an eigenvector problem. Various algorithms (the most common are Singular Value Decomposition SVD and the NIPALS algorithm) can be used to find the eigenvectors and the correspondent eigen – values of a matrix. The eigenvector with the highest eigenvalue will be PC1, the eigenvector with the second highest eigenvalue will become PC2, and so on.

PCA decomposes the original matrix X (absorbances) in a Matrix P called loadings-matrix and a matrix T, called scores-matrix. The loadingsmatrix P is a transformation matrix which rotates the reference system, while the scores-matrix T contains the projections of the original data onto the new reference system. PCA, therefore, allows the drastic reduction of the dimen – sionality of the system without significant loss of information since usually few PCs are needed to describe most of the variance in the data, so that the less important PCs can be neglected while building a model. The PCA system can be described by Equation 2 and is further graphically illustrated in Figure 1.

Eq 2

The PCA as defined by Equation 2 contains only spectroscopic data, here represented by the absorbance matrix X. However, if we want to perform quantitative analysis to determine unknown concentrations by spectroscopic methods, we need to establish a correlation between the measured spectra and the con – centrations, here represented by the vector y (components yi). This can be achieved through a regression calculation, Equation 3, which allows us to establish a correlation between the y (concentration) and the original X-variables (spectra), where b contains the regression coefficients.

Eq 3

If, however, instead of considering the original data X, we can use the data obtained from the PCA to obtain Equation 4, which is analogeous to Equation 3 but uses the scores of the PCA (matrix T). Equation 4 becomes the equation for the PCR that regresses the y data on the PCs of the PCA, thereby providing different regression coefficients q.

Eq 4

In order to be able to use Equation 4 to perform quantitative analysis, we have to determine the regression coefficients q. This can be achieved through a calibration where both y data and X data have to be known; each row of the matrix Y contains the calibration concentrations of each calibration sample, through which we obtain Equation 5.

Eq 5

It is now to use the coefficients q and the loadings P that were determined in the calibration in order to predict the concentration y of an unknown sample from its absorption spectrum using Equation 6.

Eq 6

Both PCA and PCR transform the X data and work with the original concentration data y. PLS goes one step further and also transforms the y data, performing a PCA on them. PCR and PLS have similar predicting powers and the accuracy and precision of these two methods are closely related although PLS usually requires fewer coordinates than PCR. More detailed discussion of the mathematical background of PCA, PCR and PLS can be found in the literature11-13. Although there is a variety of chemometrics software commercially available offering various data pre-treatments and multivariate methods, they are not a prerequisite to perform multivariate calibration; basic PCA and PCR methods can easily be programmed using mathematical software such as Matlab or GNU Octave.

Experimental

The chocolate samples, dark chocolate (8 samples) and milk chocolate (3 samples), as well as the reference values of the fat, protein, sugar and water content were provided by Max Felchlin AG. The reference values were determined by an external laboratory specialised in quantitative analysis using standardised methods1. For each sample, three independent measurements were performed and each measurement was treated as an independent sample. Two measurements were used to calibrate the PLS model, while the third was used to create a validation set. The calibration set, therefore, contained 22 samples, while the validation set was formed from 11 samples. The NIR spectra were measured at 50°C using a Bruker MPA-NIRspectrometer. The multivariate models were computed using The Unscrambler X14.

Results

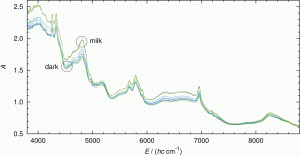
Figure 2: The NIR spectra (without pre-treatment) plotted as absorption A against wavenumber v~ (in cm-1) here given as energy E divided by the product of Planck’s constant h and the velocity of light c, see also7. The upper lines (3 spectra) belong to milk chocolate whereas the lower lines belong to dark chocolate (8 spectra)

Typical measured spectra are represented in Figure 2. It is clearly visible that spectra of dark chocolate and milk chocolate tend to form separate groups of spectra, which can be easily held apart. This is even more obvious when we look at the score plot of the PCA in Figure 3, where a clear separation between dark and milk chocolate clusters can be seen.

Figure 3: Score values for the untreated spectra on PC1 and PC2. Milk and dark chocolate are clearly separated

In order to compensate different scattering by dark and milk chocolate, the spectra were treated with Extended Multiplicative Scatter Correction (EMSC). EMSC is a method developed to correct multiplicative and additive effects caused by different light scattering in the spectroscopic measurement. In our case, EMSC is used to correct scattering differences for dark and milk chocolate.

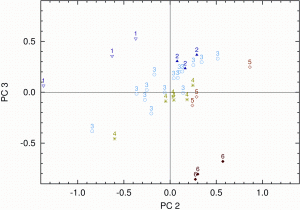
Figure 4: Score values related to fat content for the EMSC pre-treated spectra on PC2 and PC3. Numbers and colours identify samples according to their fat content (1: 31.8, 2: 36.0 to 36.9, 3: 37.3 to 37.4, 4: 38.5 to 40.4, 5: 42.6, 6: 46.5 per cent)

Figure 4 shows the score values of the EMSC pre-treated spectra on PC2 and on PC3. In order to highlight the correlation between content of fat and score values of the PCA, the samples were grouped according to their fat content. The score plot clearly shows a pattern and a correlation between fat content and score values. Samples having the lowest fat content show negative score values on PC2 and rather high scores on PC3 (for example No. 1). In contrast, the higher the fat content, the more positive the scores on PC2 and the lower the scores on PC3 (for example No. 6). Similar patterns were found in the score plot PC1 against PC2 for sugar content and less pronounced for protein content (not shown here). However, neither the score plots PC1 against PC2 represented in Figure 5 nor PC3 against PC4 show a correlation between score values and water content of the sample.

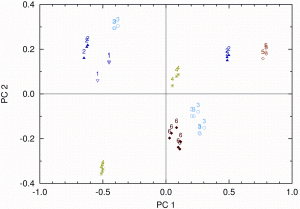
Figure 5: Score values related to water content for the EMSC pre-treated spectra on PC1 and PC2. Numbers and colours identify samples according to their water content (1: 0.47, 2: 0.65, 3: 0.71, 4: 0.8 to 0.92, 5: 1.12, 6: 1.31 per cent)

Individual PLS regression models were computed for each constituent of chocolate with four different calibrations. For the first calibration, the untreated, original spectra were used. The second calibration was modelled using the EMSC pre-treated spectra. The inspection of the X-loadings of the second calibration suggested that the spectral range between 8850 and 12500 cm-1 does not contain information relevant to the quantification of fat, protein, sugar and water (see Figure 6).

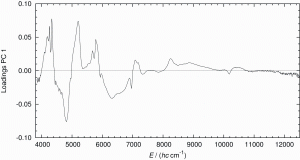
Figure 6: Loadings versus wavenumber for PC1 (obtained with PCA including pre-treatment EMSC, see Table 2) suggest that the spectral range above 8850 cm-1 does not contain significant information for the quantification of the four constituents

Thus, a third calibration was created using the range between 3,500 and 8,850cm-1 of the EMSC-treated spectra. Due to the obvious discrepancy between the spectra of dark and milk chocolate, a fourth calibration was generated considering only samples of dark chocolate. A calibration only with milk chocolate was not prepared because of a lack of a sufficient number of samples. The parameters relevant for the four calibrations are summarised in Table 2.

table 2

The predictive power of each calibration was then examined with a cross-validation by predicting the contents of analyte of the samples in the validation set. For each constituent of chocolate it was possible to set up multiple models that offered satisfactory predicting power. Calibration No. 4 (only dark chocolate, see Table 2) provided the best predictions for protein, sugar and water.

table 3

The fat content was best predicted by calibration No. 3 (cropped spectra, see Table 2). The relative root mean square error of the prediction (rel-RMSEP) for water, fat, protein, and sugar lie between 0.6 and 4.7 per cent. Considering the limited data set, the quality of our model presented here is supported by the slope, the offset and by the correlation coefficient squared given in Table 3 which summarises all the values of the prediction diagnostics for the best calibrations. Table 4 shows that our results confirm or exceed the expected precision.

table 4

It is to be noted that the investigations listed here used either chocolate mass, finished chocolate or even cocoa powder and this might influence the quality of the NIR spectroscopic determination as well. The combination of NIR and IR in the study of chocolate powder gives very low relative RMSEP values4, which might be due to the special matrix compared to chocolate mass investigated at 40 to 50°C3,5,6.

While calibration for fat, protein and sugar achieve very low relative RMPES (error of prediction), the relative precision of the prediction of water content is higher which implies that the water content is less well determined. Firstly, this is because of the low absolute value of the average water content. Secondly, the abovementioned lack of correlation between water content and scores is already a hint that a fit might be difficult or unreliable. The quality of prediction for water could possibly be enhanced by improving the analytical reference method or by a different pre-treatment of the data. Frequently, one uses as another possible pre-treatment the first or second derivative of the NIR spectra3-5. In our case, we could not find any significant improve – ment with respect to the procedure described above. In some cases, outlier detection is important, especially in monitoring production processes over a long period of time, because drift effects might influence the analysis. Outlier detection helps to detect when re-calibration is needed15.

Conclusion

This study demonstrated that it is possible to determine the content of fat, protein, sugar and water in chocolate by means of NIR spectroscopy combined with chemometric methods. The results obtained are consistent with the findings of similar previous investiga – tions2-6 and confirm that NIR is a viable tool to quickly determine the content of chocolate with respect to the four constituents fat, protein, sugar, and water. Although wet chemical methods will always be used for external independent calibration, NIR offers a suitable and efficient replacement. Moreover, modern NIR spectrometer are relatively easy to use and the measurements can be carried out by technical staff without extensive training, thus making it an ideal tool for repeated measure – ments during the production process. However, an important prerequisite is a thorough understanding of the first principles of chemo – metrics as well as IR spectroscopy.

References

1. The International Office of Cocoa, Chocolate and Sugar Confectionery (IOCCC) made a collection of analytical methods available. IOCCC has been renamed to International Confectionary Association ICA, see http://www.international-confectionery.com

2. Davies, A. M. C, Franklin, J. G., Grant, A., Griffiths, N. M., Shepherd, R., Fenwick, G. R., “Prediction of chocolate quality from near-infrared spectroscopic measurements of the raw cocoa beans”, Vibr. Spectrosc. 2, 161 (1991)

3. Tarkosova, J. and Copikova, J., “Fourier transform near infrared spectroscopy applied to analysis of chocolate”, J. Near Infrared Spectrosc. 8, 251 (2000)

4. Vesela, A., Barros, A. S., Synytsya, A., Delgadillo, I., Copikova, J. and Coimbra, M. A., “Infrared spectroscopy and outer product analysis for quantification of fat, nitrogen, and moisture of cocoa powder”, Anal. Chim. Acta 601, 77 (2007)

5. Moros, J., Inon, F. A., Garrigues, S. and de la Guardia, M., “Near-infrared diffuse reflectance spectroscopy and neural networks for measuring nutritional parameters in chocolate samples”, Anal. Chim. Acta 584, 215 (2007)

6. da Costa Filho, P. A., “Rapid determination of sucrose in chocolate mass using near infrared spectroscopy”, Anal. Chim. Acta 631, 206 (2009)

7. Cohen, E. R., Cvitas, T., Frey, J. G., Holmström, B., Kuchitsu, K., Marquardt, R., Mills, I., Pavese, F., Quack, M., Stohner, J., Strauss, H. L., Takami, M. and Thor, A. J., Quantities, Units and Symbols in Physical Chemistry, 3rd Edition, 3rd Printing, IUPAC & Royal Society of Chemistry, Cambridge (2011); see also http://www.iupac.org

8. van de Waterbeemd, H., Carter, R. E., Grassy, G., Kubinyi, H., Martin, Y. C., Tute, M. S. and Willett, P., “Glossary of terms used in computational drug design. IUPAC Recommendations 1997”, Pure Appl. Chem. 69, 1137 (1997)

9. Wold, S., “Chemometrics; what do we mean with it, and what do we want from it?”, Chemom. Intell. Lab. Syst. 30, 109 (1995)

10. Wold, S., Sjöström, M., “Chemometrics, present and future success”, Intell. Lab. Syst. 44, 3 (1998)

11. Kramer, R., Chemometric Techniques for quantitative analysis, Marcel-Dekker Inc., New York (1998)

12. Otto, M. Chemometrics, 2nd Edition, WILEY-VCH, Weinheim (2007)

13. Wold, S., Sjöström, M. and Eriksson, L., “PLS-regression: a basic tool of chemometrics”, Chemom. Intell. Lab. Syst. 58, 109 (2001)

14. The Undscrambler X, see http://www.camo.com.

15. Small, G. W., “Chemometrics and near-infrared spectroscopy: Avoiding the pitfalls”, Trends Anal. Chem. 25, 1057 (2006)

About the author

Professor Dr. Jürgen Stohner FRSC is Head of the Physical Chemistry group of the Zürich University of Applied Sciences (ZHAW) in Wädenswil, Switzerland. His current research interest focuses on the high- and low-resolution infrared spectroscopy of small (chiral) molecules, vibrational circular dichroism spectroscopy and it’s ab initio calculation and interpretation. He is head of the specialisation ‘Chemistry for the Life Sciences’ in the Master’s program Life Sciences. Since 2011, Professor Stohner has been the Chairman of the IUPAC Commission on Physicochemical Symbols, Terminology, and Units as well as Secretary of ICTNS, the Interdivisional Committee on Terminology, Nomenclature and Symbols. In 2012, he was appointed Fellow of the Royal Society of Chemistry, London.

Professor Stohner received his PhD from the Swiss Federal Institute of Technology in 1994 on the ‘Quantum dyanmics of the infrared multiphoton excited CH chromophor in molecules of low symmetry’ (Examiner: Professor Dr. Martin Quack, Co-examiner: Professor Dr. Richard R. Ernst). He was post-doc at the Université de Montréal, Canada, in the research group of Professor Tucker Carrington Jr. and worked on theoretical spectroscopy. Since 1998, he has been a lecturer for Physical Chemistry, now at the Institute of Chemistry and Biological Chemistry (ZHAW). He is the author of about 40 scientific contributions, among which is the IUPAC Green Book