Refrigeration: A deep dive into the deep freeze

In ice cream small round ice crystals are important for a soft and creamy texture. In general, it holds that the faster the freezing rate the smaller the ice crystal size. Yet for some food materials there is an upper limit for the freezing rate. If freezing is too fast, mechanical stresses are imparted to the food material and freeze fracturing can occur. In a few cases the freezing process is used to structure materials, such as the traditional Japanese kori-tofu dish, or scaffolds as used in biological tissue engineering. A few years ago WUR, together with TU Delft and Unilever, investigated the use of freeze-drying to structure soup vegetables. Here, the ice crystal size determines the size of the pore space after drying, and helps with rehydration of the vegetables when mixed with the soup.

Relation between ice crystal size and freezing rate

Hence, from the perspective of frozen food quality, it is important to have good knowledge about the relationship between ice crystal size and freezing rate. However, there exist only some empirical relations between freezing rate and ice crystal size . Also, for manufactured foods there are some other means used to control ice crystal size, such as cryopectants like sugars and anti-freeze proteins. This indicates that one can expect an interaction between food material composition, freezing rate and ice crystal size, yet in the empirical relations the dependence on food composition is absent. Therefore, Food & Biobased Research has engaged a research project targeted into a more theoretical understanding of the relationship between freezing rate, composition and ice crystal size using advanced computer simulations.

Phase field model for ice crystal growth

To obtain this detail of understanding we must dive into the micrometre range of food microstructure, where individual ice crystals are resolved in the computer model developed, where crystal growth is modelled as a function of matrix composition. The most advanced method in this field is the phase field model, which we have utilised to describe the structuring of dispersions like foams and emulsions, stabilised with emulsifiers. In the phase field method one can simultaneously model several individual elements of dispersions, such as emulsion droplets, foam bubbles and crystals. The method easily allows for break-up and coalescence of these dispersed elements.

The strength of the method lies in how it treats the interface between dispersed and continuous phases. Here, the method follows the proposal of a famous Dutch physicist, vanderWaals, to include the interface in a thermodynamic framework. Using the phase field method we have constructed a computer model for the description of ice crystals in a sucrose solution, whose behaviour can be viewed as representative for ice cream³. In earlier research we have already clarified the thermodynamics of aqueous sucrose solutions⁴, and also the speed of water transport in sugar solution via diffusion⁵. Thus, for these material properties we have predictive theories available as function of sucrose concentration for the whole range from 0 to 100%.

Freeze rate, composition and ice crystal size

After having developed the computer model, we performed several computer simulations to investigate the relationship between freezing rate, composition and ice crystal size. We zoomed into a small part of the food material and seeded several nuclei for ice crystals to grow. This part of food material was then subjected to a range of freezing rates. Simulations were performed for two different sucrose concentrations – and a multitude of different random positions of the nuclei – in order to obtain some good statistics.

Snapshots of these computer simulations are shown in Figure 1. The dark blue dispersed elements are individual ice crystals. The freezing rate is not very fast, so we can assume that the ice crystals remain approximately spherical. For understanding of the simulation results it is important to know that ice crystals do not contain sugar, so the growth of ice crystals implies the increase of sugar concentrations in the unfrozen phase. The increased sugar concentration leads to an increase of the freezing point, leaving the continuous matrix unfrozen.

Figure 1: Snapshots of ice crystal growth in a sugar solution obtained via computer simulations for different freezing rates (0.01, 0.03 and 0.10 K/s from top to bottom) observed at different times (from left to right). Observe the coalescence of several ice crystals, especially at the low freezing rate (top)

Upon further freezing the ice crystals can impinge on each other, prompting an enhancement of the sugar concentration in the unfrozen liquid in between them, leading to freezing point depression. Hence, a flat interface is developed. If the freezing rate is too slow, the sugars have time to diffuse out of the impingement zone and the crystals can coalesce. In the early stage of freezing, where the local increase of sugar concentration due to ice crystal growth is small, there are several coalescence events. In the later stage of freezing, the unfrozen matrix approaches the glassy state – where the diffusion of water and sugar grinds to a halt and ice crystal growth stops.

From the simulations we have determined the average ice crystal size and have plotted this against the imposed freezing rate for two different sucrose concentrations. These results are shown in Figure 2.

Considerable scatter can be observed in the simulation data, due to the stochastics of the nucleation process. However, by performing many simulation runs, one can fit a reliable power law relation through the data, which are displayed as the lines running through the data points in Figure 2 (page 00). The fitting shows that exponents of the power law are 0.31 and 0.18 for 10% and 15% initial sugar concentration, respectively. Our earlier empirical relationship has a power law exponent of 0.25, which was assumed to be composition independent. The fact that the empirical value is quite close to the exponents we have found via simulation is very encouraging. Furthermore, it is worth noting that the simulation model did not require any parameter fitting, as all material and thermodynamic properties are known.

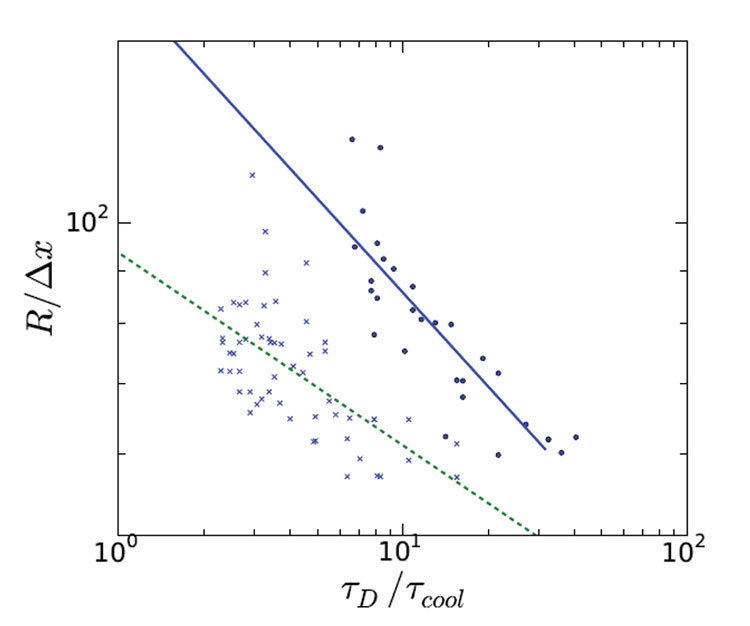
Figure 2: Average ice crystal size versus the freezing rate, for two different initial sugar concentrations (10% and 15%, indicated by solid and dashed line). The radius is measured in units of the computational mesh, which is about 3 micron, and the freezing rate 1/t_cool is measured in terms of the rate of water diffusion 1/t_D. (at 0.01K/s if t_D/t_cool=1) The points indicate the average size of a single simulation. The lines represented power law relations, fitted to the simulation data

Food quality issues for frozen fruits and vegetables

Food & Biobased Research concludes that the model does have a large degree of realism. Moreover, similar predictive theories on material and thermodynamic properties are available for many other food materials. Consequently the model is, in principle, applicable to a multitude of other food materials. On this basis we have launched a new research project that continues to develop and adapt the model to frozen food materials with a cellular structure to investigate frozen food quality issues for fruits and vegetables. The phase field model will be embedded in a multiscale model – because in food products local differences in freezing rate will arise – which must be resolved with an advanced approach, where the temperature profile is computed at the product scale, and the ice crystal growth at the microscale. The macroscale computer model will call the microscale model multiple times for a multitude of locations. The microscale model will report back the local ice fraction, while the macroscale model will issue the applied temperature gradient to the microscale model.

In this new project, Food & Biobased Research, we will not only focus on the initial freezing step, but also on the frozen storage. During storage temperature fluctuations can occur due to the mechanical cooling, or door opening and closing. It is assumed that these temperature fluctuations allow ice crystals to grow further, which is disadvantageous for the product quality⁶. We aim to investigate whether lowering the storage temperature makes the food less sensitive to temperature fluctuations, and even whether reduction in energy usage can be obtained. Moreover, even where storage temperature is reasonably constant, there is still coarsening of ice crystal distribution occurring during storage at the conventional conditions of -18^oC. This is shown in the comparison of food frozen via airblast freezing and Pressure Shift Freezing (PSF). Initially, the ice crystal size obtained via PSF is much smaller than obtained via convential airblast freezing. However, after several weeks of storage little difference in the final ice crystal size distribution is found, indicating that coarsening has happened during storage of PSF foods⁷.

In summary, the new simulation model is an essential tool to dive into possible means for the frozen foods industry to control frozen food texture and ice crystal size, in areas such as 1) product formulation, 2) processing conditions and freezing rate. Knowing the impact of formulation and processing on frozen food quality, novel strategies for frozen storage can be evaluated due to their impact on both product quality and energy savings.

References

1. Voda, A., Homan, N., Witek, M., Duijster, A., van Dalen, G., van der Sman, R., Nijsse, J, van Vliet, L. Van As, H. & van Duynhoven, J. (2012). The impact of freeze-drying on microstructure and rehydration properties of carrot. Food Research International, 49(2), 687-693
2. van der Sman, R. G. M., Voda, A., van Dalen, G., & Duijster, A. (2013). Ice crystal interspacing in frozen foods. Journal of Food Engineering, 116(2), 622-626
3. van der Sman, R. G. M. (2016). Phase field simulations of ice crystal growth in sugar solutions. International Journal of Heat and Mass Transfer, 95, 153-161
4. van der Sman, R. G. M., & Meinders, M. B. J. (2011). Prediction of the state diagram of starch water mixtures using the Flory–Huggins free volume theory. Soft Matter, 7(2), 429-442
5. van der Sman, R. G. M., & Meinders, M. B. J. (2013). Moisture diffusivity in food materials. Food chemistry, 138(2), 1265-1274
6. Regand, A & Goff HD. “Structure and ice recrystallization in frozen stabilized ice cream model systems.” Food Hydrocolloids1 (2003): 95-102
7. Fernández PP, Otero L, Martino MM ,Molina-García AD, & Sanz PD “High-pressure shift freezing: recrystallization during storage” European Food Research and Technology 5 (2008): 1367-1377

About the author

Ruud van der Sman has an MSc in Applied Physics at Delft University of Technology and a PhD in Agricultural Engineering from Wageningen University. He works as a senior researcher at Food & Biobased Research, and part-time assistant professor at Food Process Engineering – both part of Wageningen UR (University & Research centre). His research interests comprise of soft matter physics of food materials, computer modelling of food structuring at the micrometre scale, and physiology modelling. His expertise in meat comprises of thermodynamics of water holding capacity, heat and mass transfer and post-mortem physiology. www.wageningenur.nl/en/fbr